Learning Made Easy

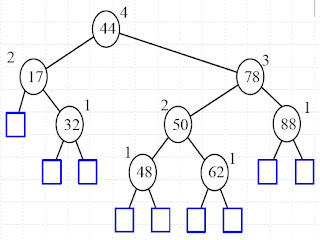
AVL Trees =============== - Also called height balanced tree -Height of children present at same level may not have same height. There height can differ at most by 1. -The height of an AVL tree T storing n keys is O(log n) Structure of AVL Tree ======================== - Consoder an AVL tree of n nodes -Cosider a leaf which is closest to the root - Suppose this leaf is at level k. -Then height of a tree is at most 2k - 1. Summary of AVL Tree ========================== - If height is h , then leaf closest to root is at level  at least (h+1)/2 -On the first (h-1)/2 levels the AVL tree is a complete binary tree - After (h-1)/2 level the AVL tree may start "thinning out" -Number of nodes in AVL tree is at least 2 to raise (h-1)/2 and at most 2 raise to h Insertion in AVL Tree ========================== Insertion of node make tree changes height and hence height balance property voilated. If Insertion causes T to become unbalanced , we travel up the ...

Definition: A  binary tree       T  is a finite set of  nodes    with the following properties: Either the set is empty,  ; or The set consists of a root,  r , and exactly two distinct binary trees   and  ,  . The tree   is called the  left subtree    of  T , and the tree   is called the  right subtree    of  T . They are considered as Ordered subtrees. Level i has   2 i    nodes. In a tree of height h, Leaves are level at h. No of leave are    2 h. No of internal nodes  2 h      -1. No of internal nodes = no of leaves -1 Total no of nodes =  2 h+1   -1 =n In a tree on n nodes  No of leaves is (n+1)/2 height =    Log 2 (n+1)/2 Tree Traversal PostOrder Traversal PreOrder  Traversal InOrder  Traversal PostOrder Traversal...

Running time of an algorithm, order of growth.  Worst case.   Running time of an algorithm  increases with the size of the input in the limit as the size of the input increases without bound. Big-theta notation (a=b) g(n) is an asymptotically   tight bound of f(n). Asymptotically non negative/positive. If g(n) is asymptotically negative then theta(g(n)) = empty.  Example 1/2n2 - 3n= theta(n2). Big O-notation (a<=b) Asymptotic upper bound Not tight bound  Theta is stronger than O O notation describe upper bound on every input. We also have amortized analysis.[An amortized analysis is any strategy for analyzing a sequence of perations to show that the average cost per operation is small, even though a single operation within the sequence might be expensive] ] Example The running time is O(n2) means there is a function f(n) that is O(n2) such that for any value of n, no matter what ...

Whenever the word "Gate" comes in my mind , it always reminds me one thing " Jo bhi faltugiri ki Engg me bhul jao, Now its time to be serious. "  Gate is one most important exam from my point of view. It is like mirror that tells you what you have studied throughout engineering. It tells you whether you were really serious  or it was  just the TechMax which helped you to overcome your hurdles. Most of the gate questions comes from following subjects... 1.Data Structures including Graph theory,Algorithms  etc...it looks easy but really needs to be studied thoroughly.  2. Theory of computation science , in this parser part you should understand properly. 3. Math its one of my favourite ..No comments on this. 4. DataBase System looks very easy but you should all concepts of it. 5. At the End COA ,CN ,OS SA , it hate all these subjects  ,  specially CN, but still we have to study. Gate is not a difficult exam, So just chill maro yaar.....